Two-Dimensional Arrays

Section 1: Introduction

While one-dimensional arrays resemble lists, two-dimensional arrays resemble a table or matrix with rows and columns. Technically, JavaScript doesn't support multi-dimensional arrays, but you can simulate a two-dimensional array by creating an array of arrays.

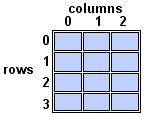
Section 2: Declaration

Multi-dimensional arrays can be declared in a variety of ways. If you know in advance the data that you are planning to store in the array then you can declare the array as in the example below.

var testArray1 = [ [' ', 'April', 'May', 'June'],             // row 1
['Store #2', 4400, 4100, 3400],    // row 2
['Store #3', 2700, 2985, 3200],    // row 3
['Store #4', 2200, 2485, 2900] ]; // row 4

See demo, test 1.

If you don't have the data but know how many rows and columns you need, you can declare it as follows. The code below sets up an array with three rows and four columns:

var testArray1 = [];

// Can set up rows as arrays like this. The following lines
// indicate that there are three rows, and each one is an array:
testArray1[0] = [];
testArray1[1] = [];
testArray1[2] = [];

// Now we have to specify the number of columns in each row:
// Each row can have a different number of columns, but we'll assign uniform size for all
testArray1[0].length = 4;
testArray1[1].length = 4;
testArray1[2].length = 4;

See demo, test 2.

You can also declare the same array as follows, using a loop:

var testArray1 = [];
testArray1.length = 3;

// loop through all rows, setting uniform size for columns
for (rowCtr = 0; rowCtr < testArray1.length; rowCtr++)
{
testArray1[rowCtr] = [];
testArray1[rowCtr].length = 4;
}

See demo, test 3.

testArray1 (as defined above)

Array testArray1 is a 2-dimensional array with 4 rows and 3 columns – or 12 elements.

Section 3: Accessing Elements and the for Loop

Elements in 2-D arrays are referred to by the array variable name and two indexes – one for each dimension.

Examples:

testArray1 [3][2]

testArray1 [3][J]

testArray1 [M][J]

testArray1 [N+1][J]

Using the declaration above, along with the following declarations:

var rowCtr, colCtr;

the program segment below will create a portion of a multiplication table:

for (rowCtr = 0; rowCtr < testArray1.length; rowCtr++)
{
for (colCtr = 0; colCtr < testArray1[0].length; colCtr++)
{
testArray1[rowCtr][colCtr] = rowCtr * colCtr;
}
}

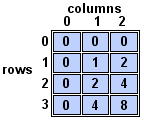
Notice that one row was processed at a time. Since the loop that contained rowCtr as a loop control variable was the outermost loop, the inner loop was processed completely for each increment of rowCtr, i.e., rowCtr =0: colCtr = 1, 2, 3; rowCtr = 1: colCtr = 1, 2, 3; etc. In nested loops the innermost loop runs faster.

Section 4: while Loop

for loops are ideal for processing an entire array. However, if you want to stop processing when a certain condition is met then the for loop should not be used. The for loop is a count-controlled loop, and should include no additional terminating conditions. In such cases a while loop is preferable.

The following code demonstrates the necessity of the while loop. It creates a partial multiplication table from a 5 x 5 array with the added restriction that the results can be no more than single digits:

var singleDigit;
var product;
for (rowCtr = 0; rowCtr < prod.length; rowCtr++)
{
colCtr = 0;
singleDigit = true;
while ((colCtr < prod[0].length) && singleDigit)
{
product = rowCtr * colCtr;
if (product < 10)
{
prod[rowCtr][colCtr] = product;
}
else
{
singleDigit = false;
}
colCtr += 1;
}
}

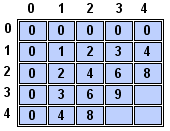
See demo, test 4.

Section 5: length

Although it should be apparent from the preceding examples, the length can be used to determine the length for both the rows and columns.

row dimension:

testArray1.length

column dimension:

testArray1[0].length

The column dimension makes the assumption that all columns are the same size. That is not a requirement, but is fairly normal.

Section 6: Initialization

The following declaration...

var salesArray = [ [2200, 1000, 3000, 1000],
[2100, 1000, 3000, 2000],
[2300, 1000, 3000, 3000] ];

...results in an array that looks like this:

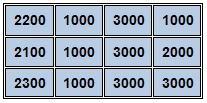
You can also populate an array through code:

See demo, test 5.

Section 7: Array Processing

Access all elements row-by-row

for (rowCtr = 0; rowCtr < testArray.length; rowCtr++)
{
for (colCtr = 0; colCtr < testArray[0].length; colCtr++)
{
// Process testArray[rowCtr][colCtr]
}
}

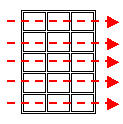
Access all elements column-by-column

for (colCtr = 0; colCtr < testArray[0].length; colCtr++)
{
for (rowCtr = 0; rowCtr < testArray.length; rowCtr++)
{
// Process testArray[rowCtr][colCtr]
}
}

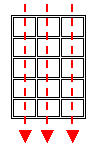
Access a random element

testArray[rowCtr][colCtr]

Process a single row (rowCtr is held constant while colCtr changes)

rowCtr = <some value>;
for (colCtr = 0; colCtr < testArray[0].length; colCtr++)
{
// Process testArray[rowCtr][colCtr]
}
}

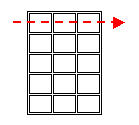
Process a single column (colCtr is held constant while rowCtr changes)

colCtr = <some value>;
for (rowCtr = 0; rowCtr < testArray[0].length; rowCtr++)
{
// Process testArray[rowCtr][colCtr]
}
}

Image of Processing a Single Table Column.

Process a diagonal from left to right

First determine the smallest upper bound and store it in a variable called limit

if (testArray.length < testArray[0].length)
{
limit = testArray.length;
}
else
{
limit = testArray[0].length;
}

...or...

limit = (testArray.length < testArray[0].length ? testArray.length : testArray[0].length);

Next, loop diagonally...

for (var diag = 0; diag < limit; diag++)
{
// Process testArray[diag][diag]
}

Process a diagonal from right to left

Again, first determine the smallest upper bound and store it in a variable called limit

if (testArray.length < testArray[0].length)
{
limit = testArray.length;
}
else
{
limit = testArray[0].length;
}

...or...

limit = (testArray.length < testArray[0].length ? testArray.length : testArray[0].length);

Next, loop diagonally...

for (var diag = 0; diag < limit; diag++)
{
// Process testArray[limit - diag]
}

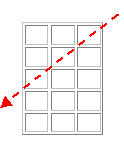
See demo, test 6.

Section 8: Multi-Dimensional Arrays

You can create arrays with more than two dimensions. The number of dimensions of an array is the same as the number of indexes needed to reference a particular cell.

This example stores a cube of data, in effect, two sets of row and columns, or three dimensional data.

var cubeArray = [ [ [ 1, 2], [ 3, 4], [ 5, 6] ],
[ [ 7, 8], [ 9,10], [11,12] ],
[ [13,14], [15,16], [17,18] ],
[ [19,20], [21,22],[23,24] ] ];

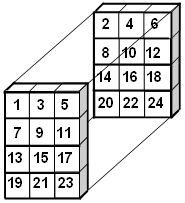
The total number of elements is the product of the number of elements in each dimension of the array, in this case 4 rows x 3 columns x 2 deep, or 24 elements.

One way to keep track of where you are in a multi-dimensional array is to let the first subscript (left-hand one) be referenced by the outermost loop, the second subscript by the next to the outermost loop, etc., until the last subscript is referenced by the innermost loop.

for (rowCtr = 0; rowCtr < cubeArray.length; rowCtr++)
{
for (colCtr = 0; colCtr < cubeArray[0].length; colCtr++)
{
for (depthCtr = 0; depthCtr < cubeArray[0][0].length; depthCtr++)
{
outputString += cubeArray[rowCtr][colCtr][depthCtr] + " ";
}
outputString += "\n";
}
}

Note that the depthCtr, or innermost loop, varies most rapidly, then the colCtr, then the rowCtr.

See demo, test 7.

Multi-Dimensional Arrays and Procedures

With regard to parameter passing and functions, passing and receiving a multi-dimensional is no different than a single-dimensional array.

Section 9: Extra Info: Beyond the Third Dimension

There are three conventional spatial dimensions: length (or depth), width, and height, often expressed as x, y and z. The fourth dimension is often identified with time in physics. It has been speculated that the fifth dimension is energy or gravity.

In geometry, the tesseract, also called 8-cell or octachoron, is the four-dimensional analog of the (three-dimensional) cube, where motion along the fourth dimension is often a representation for bounded transformations of the cube through time.

The following image is a static view of a hypercube, or tesseract.

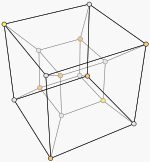
Below is an animated 3D projection of an 8-cell, or tesseract, performing a double rotation about two orthogonal planes.

Finally, the animated image below is 3D projection of an 8-cell performing a 3D projection of an 8-cell performing a simple rotation about a plane that bisects the figure from front-left to back-right and top to bottom.

Links

Wikipedia: Fourth Dimension
Wikipedia: Fifth Dimension
Wikipedia: Tesseract
"Let me sit down for a moment and then I'll be on my way. Speaking of ways, by the way, there is such a thing as a tesseract." (A Wrinkle in Time)

Section 10: Resources

Best:

Others: