Section 0: Module Objectives or Competencies
| Course Objective or Competency | Module Objectives or Competency |
|---|---|
| The student will be able to explain and apply the relational algebra operators and explain how they provide the theoretical foundation for relational databases and SQL. | The student will be able to explain and apply the relational algebra set operators. |
| The student will be able to explain and apply the specialized relational algebra relational database operators. |
Section 1: Justification
Overview
Relational algebra is very important for several reasons:
- it provides a deeper understanding of the relational model.
- it provides a formal foundation for relational model operations and SQL.
- it is used as a basis for implementing and optimizing queries in the query processing and optimization modules that are integral parts of relational database management systems (RDBMSs).
- some of its concepts are incorporated into the SQL standard query language for RDBMSs.
Justification
The core of the relational data model is relational algebra, a formal algebra for manipulating data in that model.
- Its operations take finite relations as input and produce finite relations as output, rather than working with individual tuples.
Its operations include two groups:
- Set operations from mathematical set theory; these are applicable because each relation is defined to be a set of tuples in the formal relational model and include UNION, INTERSECTION, SET DIFFERENCE, and CARTESIAN PRODUCT (also known as CROSS PRODUCT).
- Operations developed specifically for relational databases—these include SELECT, PROJECT, and JOIN, among others.
Basis of SQL
SQL is essentially built on relational algebra. The SQL parser translates its Abstract Syntax Tree into a tree of Relational Operators that describe relational algebra operations like filtering, cartesian products, joining, set operations, sorting, expressions and projections.
These operators are further transformed according to the laws of relational algebra and optimized into physical operators that actually execute the query, that is, fetch the data from the storage engine and execute the necessary transformations against rows or columns. The declarative nature of SQL comes from its close relationship with relational algebra and the ability to map SQL clauses almost directly to relational algebra operations.
Here is an additional reference on Relational Algebra and SQL.
Section 2: Operators
Relational algebra defines the theoretical way of manipulating table contents using the following relational functions:
- UNION ∪
- INTERSECT ∩
- DIFFERENCE ‒
- SELECT σ
- PROJECT π
- PRODUCT ⨯
- JOIN ⨝
- DIVIDE ÷
The first three operations (UNION, INTERSECT, and DIFFERENCE) require that the relations to which they are applied have the same type of tuples, i.e., each table must have exactly the same columns, and the domains of those columns (the set of values that they can assume) are identical.
- In such a case the tables are union compatible.
Section 3: UNION
Here is a Venn diagram of a Union operation:
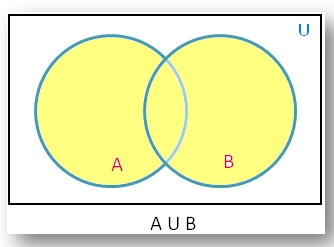
The result of the UNION operation is a new relation that includes all tuples from two tables.
- Duplicate tuples are eliminated.
- The relations must be union compatible.

Section 4: INTERSECT
Here is a Venn diagram of an Intersect operation:
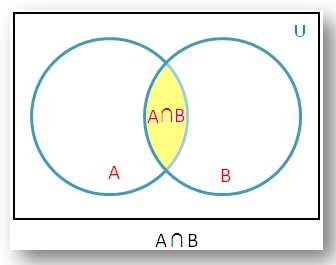 The relations must be union compatible.
The relations must be union compatible.

Section 5: DIFFERENCE
Here is a Venn diagram of an Difference operation:
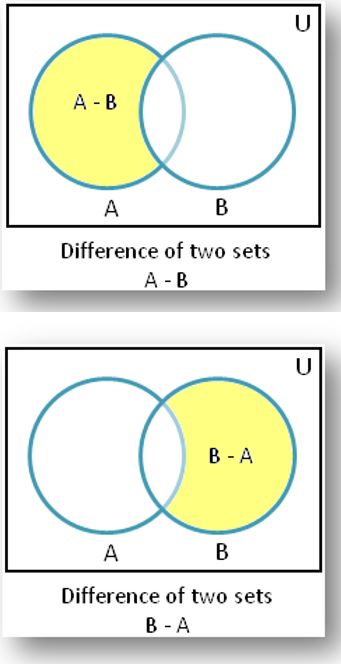 The relations must be union compatible.
The relations must be union compatible.

Section 6: SELECT
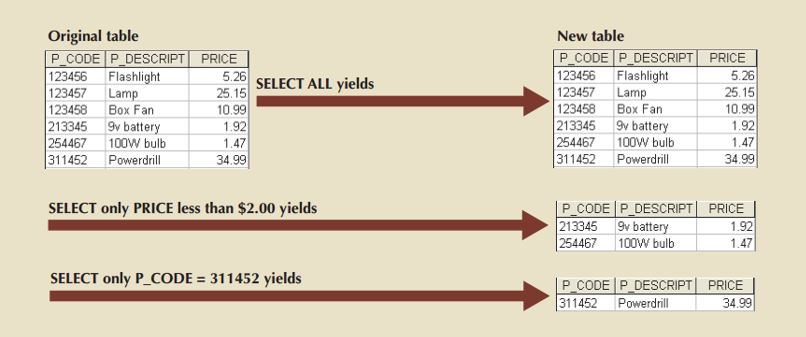
The SELECT operation can be used to list all of the row's values for each attribute found in a table, or it can select a subset of the tuples in a relation that satisfy a selection condition.
- SELECT results in a horizontal subset of a table.
Section 7: PROJECT
The results of the PROJECT operation is a list of all values for selected attributes.
- PROJECT results in a vertical subset of a table.

Section 8: PRODUCT
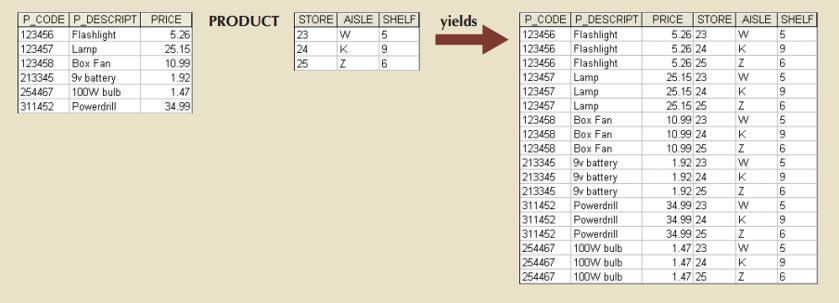
The result of PRODUCT is a relation containing a combined set of tuples from two relations, i.e., all possible pairs of rows from the two tables.
- The resulting relation will have n + m attributes, and will have one tuple for each combination of tuples.
Section 9: JOIN
The JOIN (or natural inner JOIN) operation is used to combine related tuples from two relations into single tuples.
- JOIN is the power behind a relational database.
- The following tables will be used to demonstrate:
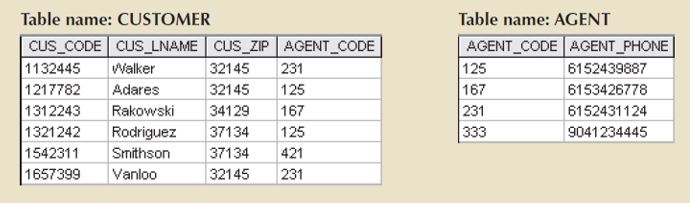
A natural JOIN links tables by selecting only the rows with common values in their common attribute.
A natural JOIN involves three steps: PRODUCT, SELECT, PROJECT).
-
PRODUCT:
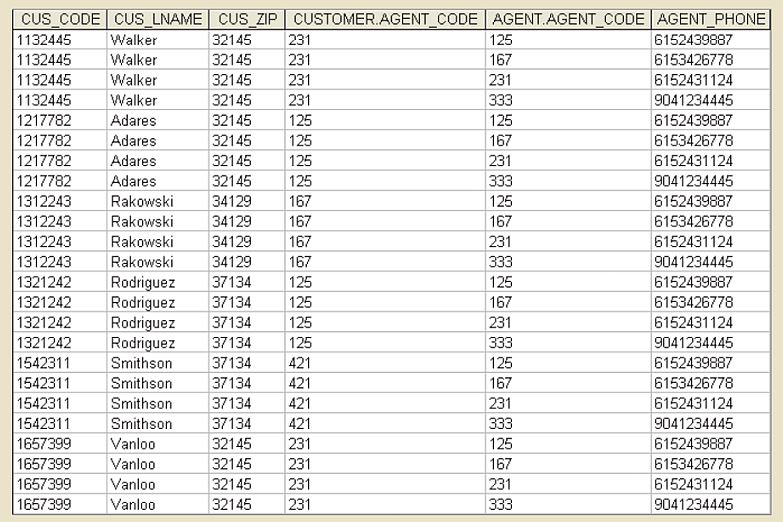
-
SELECT yields only the rows for which the AGENT_CODE values are equal:

-
PROJECT eliminates duplicate columns:
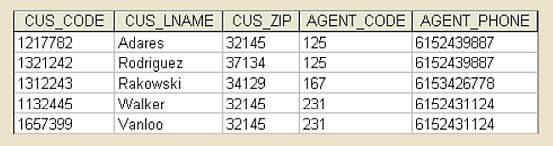
Natural JOIN notes:
- if no match is made between table rows the new table does not include the unmatched row.
- the column on which the JOIN was made occurs only once in the new table.
Another type of inner JOIN, the equiJOIN links tables based on an equality condition that compares specified attributes of each relation.
- An equiJOIN does not eliminate duplicate columns.
- The condition or criteria to join the tables must be explicitly defined.
- The result looks just like step 2 of a natural join.

An outer JOIN retains unmatched pairs and the unmatched values would be left null.
- An outer JOIN is a useful tool for checking the validity of table data.
An outer JOIN is basically an inner JOIN, but also returns extra rows padded with nulls when the JOIN condition is not satisfied.
- The result set of an outer JOIN includes all the tuples in one relation, even when some of these have no matching tuples on the second relation.
- Since the result set includes all attributes from both relations, whenever a tuple from the first relation has no matching tuple in the second relation, the result set will have a tuple with NULLs for the attributes of the second relation.
-
The outer JOIN of two relations can be interpreted as follows:
- Compute the inner JOIN of the two relations and include it in the result set of the outer JOIN of the two relations. That is, the outer JOIN result set always includes the inner JOIN result set of the two relations.
- Add to the result set the tuples from one relation that have no matching tuples in the second relation according to the JOIN condition. NULL signifies the non-existence of a matching tuple.
-
A left outer JOIN results in all the rows in the CUSTOMER table, including those that do
not have a matching value in the AGENT table.
- Note that the results reveal any customers that do not yet have an agent or have been assigned to non-existent agent (which reveals a violation of referential integrity).

-
A right outer JOIN yields all the rows in the AGENT table, including those that do not
have matching values in the CUSTOMER table.
- These results reveal any agents that have not been assigned any customers.

Section 10: DIVIDE
The DIVIDE operator is used to answer questions about one set of data being associated with ALL values of data in another set.
- The division operator is used to evaluate queries that contain the keyword ALL.
DIVIDE requires the use of one two-column table as the dividend and one single column table as the divisor.
- The resulting table is a new single column table that consists of each of the column values that has a corresponding entry in the dividend table for ALL of the entries in the divisor table.
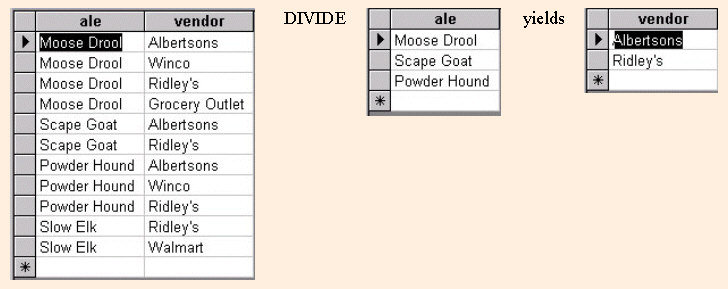
In the example below, a DIVIDE operation is used to determine which of the customers, if any, purchased every product listed in table 2.
- The table on the left shows a list of customers and the products purchased.
- Table 2 in the center contains a set of products that are of special interest to the clients, perhaps a new product line or a line of specialty products.
- The output of the DIVIDE operation on the right is a single column that contains ALL values from the second column of the dividend (CUS_CODE) that are associated with every row in the divisor.

Note the following:
- Table 1 is divided by Table 2 to produce Table 3. Tables 1 and 2 both contain the P_CODE column but do not share the CUS_CODE column.
- To be included in the resulting Table 3, a value in the unshared column (CUS_CODE) must be associated with every value in Table 2.
- The only customers associated with all of the products 123456, 234567, and 567890 are customers 10030 and 12550.
Example 2: Locating all retailers that sell a particular subset of Big Sky Brewing's product line.
- Table 1: Product Line and Retailer
- Table 2: Product Line